Saturday, January 16, 2010
The Significance of Displacement Current
Taking the divergence of the Ampere’s Circuital Law give by ▼×H = J and using the continuity equation we have
That is, equation ▼×H = J leads to steady state conditions in which charge density is not time varying function. Therefore, for time dependent fields’ ▼×H = J needs some modifications. Maxwell suggested that the definition of total current density of Ampere’s Circuital Law is incomplete and advised to add something to J. If it is assumed to be J’, we have
Since J’ arises due to the variation of electric displacement (electric flux density) D with time, it is termed as displacement current density. The modified Ampere’s Circuital Law (Maxwell’s equation), therefore, for time varying field takes the following form
Applying Stokes’s Theorem in equation (1) can be given in integral form as
The important conclusion that can be drawn now is that, since displacement current is related to the electric field, it is not possible in case of time varying fields to deal separately with electric and magnetic fields but, instead, the two fields are interlinked giving rise to electromagnetic fields. It is to be noted that, in a good conductor J’ is negligible compared to J at frequency lower than light frequencies (1015 Hz).
Maxwell's Equations and their Physical Significances
 |
| Coulomb’s and Gauss’s Laws |
 |
| Maxwell’s equations |
Maxwell's Equations in Frequency Domain
Maxwell's Equations in Phasor Form
 |
| Maxwell's Equations |
 |
| Maxwell's Equations in Phasor Form |
Electromagnetic Wave Equation or Helmholtz Equation
We will consider a linear, isotropic, homogeneous medium. Moreover, the net free charge in the source free region is zero (ρv = 0) and that any currents in the region are conduction currents (J=σE). These types of regions are quite general ones and include the practical cases of free space (σ = 0) as well as most conductors and dielectrics. Maxwell’s equations for this region:
 |
| Electromagnetic Wave Equation |
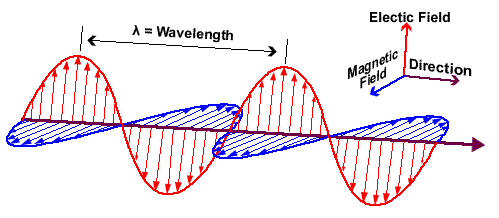
Characteeristics of a Uniform Plane Wave
Uniform plan waves satisfy the following conditions:
1. At every point in space E and H are perpendicular to each other and to the direction of propagation. No fields, therefore, in the direction of wave propagation.
2. Everywhere in space, the fields vary harmonically with time and at the same frequency.
3. Each field has the same direction, magnitude and phase at every point in any plane perpendicular to the direction of wave propagation. The fields, therefore, are only function of the coordinate that represents the direction of wave propagation.
Pointing Theorem and Explains its Various Terms
If we define the power density vector as:
P=E×H Watt/m2.
Using the Maxwell’s equations we have
Equation (1) is known as the point form of pointing theorem. Integrating both sides of (1) over some volume v and applying the divergence theorem, we obtain the integral form of pointing theorem as follows:
The term on the side of (2) is the net inward flux of P into the volume v. The First term on the right side of (2) is a power dissipation term in that it represents the rate of expenditure of energy by the electric field. The second term on the right side of (2) is given by
And represents the time rate of increase of energy stored in the magnetic and electric fields respectively in the volume v.
Therefore (2) states that the net inward flux of the pointing vector through some closed surface is the sum of the power dissipated in the volume enclosed by the surface and the rate of change of energy stored in the volume enclosed by the surface.