Maxwell's Equations and their Physical Significances

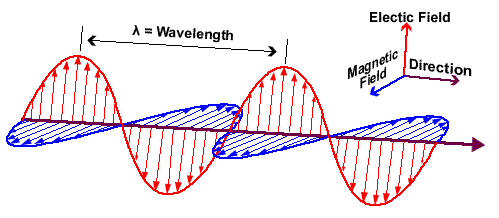
By studying the physical properties of electric (E-field) and magnetic (B-field) fields we have been able to describe these properties by four, relatively simple, equations known as Maxwell’s equations.

These four fundamental equations of electromagnetism can be expressed in both an integral and differential form as tabulated below:

Coulomb’s and Gauss’s Laws

Equation (1) results from Coulomb’s and Gauss’s Laws and states that free charges act as sources or sinks of D. It suggests that the total electric flux density or total electric displacement through the surface enclosing a volume v is equal to the total charge within the volume.

Equation (2) arises from the application of Gauss’s law to magnetic fields and the non-existence of magnetic monopoles. There are no sources or sinks of B. This equation suggests that the net magnetic flux emerging through any closed surface is zero.

Equation (3) describes Faraday’s Law of electromagnetic induction and states that an electromotance is produced in a circuit when the magnetic flux through the circuit changes. It suggests that the electromagnetic force around a closed path is equal to the time derivative of the magnetic flux density through any surface bounded by the path.

Equation (4) describes Ampere’s Circuital Law (which is derived from the Biot-Savart Law) and states that the electromotive force around a closed path is equal to the conduction current J = σE plus the time derivative of the electric flux density through any surface bounded by the path.

Maxwell’s equations

In vacuum/free space ρ_v = 0, J = 0, ε = ε_o and μ = μ_o. Therefore, in vacuum the Maxwell’s equations take the following forms: